Question

Point charge A with a charge of +3.00 μC is located at the origin. Point charge B with a charge of +6.00 μC is located on the x axis at x = 7.00 cm. And point charge C with a charge of +2.00 μC is located on the y axis at y = 6.00 cm. What is the net force (magnitude and direction) exerted on each charge by the others?

charge A magnitude

charge A direction

charge B magnitude

charge B direction

charge C magnitude

charge C direction

Answer 1

A) F_{A} = 36.26 N , θ = 204.4º

B) F_{B} = 43.45 N , θ = 349º

C) F_{C} = 25.16 N , θ = 112.52º

Step-by-step explanation:

The force is a vector quantity, so we must take into account the direction of the force, for the calculation of the electric force we will use Coulomb's law

F₁₂ = k q₁ q₂ / r₁₂²

we will use numerical indexes 1 for A, 2 for B and 3 for C

a) Force on charge A

X axis

Fₓ = F₁₂

Fₓ = k q₁ q₂ / r₁₂²

Fₓ = 8.99 10⁹ 3 10⁻⁶ 6 10⁻⁶ / 0.07 2

Fₓ = 3,302 10¹ N

Since the two charges are of the same sign, the force is repulsive, so that it is directed towards the negative side of the x-axis.

Y Axis

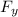`F_(y)` = F₁₃

F_{y} = k q₁q₃ / r₁₃²

F_{y} = 8.99 10⁹ 3 10⁻⁶ 2 10⁻⁶ / 0.06 2

F_{y} = 1,498 10¹ N

Repulsive force in the direction of the negative part of the y axis

To find the magnitude we use the Pythagorean Theorem

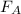`F_(A)` = √ (Fₓ² +
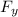`F_(y)`²)

F_{A}= √ (33.02 2 + 14.98 2)

F_{A} = 36.26 N

For the direction let's use trigonometry

tan θ = F_{y} / Fₓ

θ = tan⁻¹ F_{y} / Fₓ

θ = tan⁻¹ (-14.98 / -33.02)

θ = 24.4º in the third quadrant

Measured from the positive side of the x axis

θ = 180 + 24.4

θ = 204.4º

b) Force on charge B

X axis

Fₓ = F₂₁ + F₂₃ₓ

F₂₁ = k q₁ q₂ / r₁₂²

F₂₁ = 8.99 10⁹ 3 10⁺⁶ 6 10⁻⁶ / 0.07²

F₂₁ = - F₁₂ = 33.02 N

Directed towards the positive side of the x axis

F₂₃ = k q₃q₂ / r₃₂²

R₃₂² = (0.07² +0.06²) = 0.0085

F₂₃ = 8.99 10⁹ 2 10⁻⁶ 6 10⁻⁶ / 0.0085

F₂₃ = 1,269 10¹ N

For the direction of this repulsive force we use trigonometry

Tan θ = y / x

θ = tan⁻¹ 0.06 / 0.07

θ = 40.6º

As the force is repulsive therefore the angle is

θ = 360 - 40.6

θ = 319.4º

Now we can find the components of this force

F₂₃ₓ = F₂₃ cos 319.4

F₂₃ₓ = 12.69 cos 319.4

F₂₃ₓ = 9.635 N

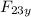`F_(23y)` = F₂₃ sin319.4

F_{23y} = 12.69 sin319.4

F_{23y} = -8.258 N

The force on this charge is

X axis

Fₓ = F₂₁ + F₂₃ₓ

Fₓ = 33.02 + 9.635

Fₓ = 42,655 N

Y Axis

F_{y} = F_{23y}

F_{y} = -8.258 N

The Magnitude is

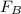`F_(B)` = √ (Fₓ² + F_{y}²)

F_{B} = √ (42,655 2 + 8,258 2)

F_{B} = 43.45 N

The address is

Tan θ = F_{y} / Fₓ

θ = tan⁺¹ (-8.258 / 42.655)

θ = -10.96

Measured from the positive side of the x axis is

θ = 360 -10.96

θ = 349º

c) The force on the charge C

X axis

Fₓ = F₃₂ₓ

Fₓ = -F₂₃ₓ = -9.635 N

Y Axis

F_{y} = F₃₁ +
`F_(32y)`

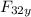
F_{y} = 14.98 + 8.258

F_{y}= 23,238 N

The magnitude is

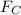`F_(C)` = √ (Fₓ² + F_{y}²)

F_{C} = √ (9,635 2+ 23,238 2)

F_{C} = 25.16 N

The address is

tan θ = F_{y} / Fₓ

θ = tan-1 (-23.238 / 9.635)

θ = -67.48

Measured from the x axis

θ = 180 -67.48

θ = 112.52º