Question

The functions f(x) = -2x + 2 and g(x) = (1/3)^x are shown in the graph.

What are the solutions to -2x + 2 = (1/3)^x + 1?
(Multiple choice)

A. -1
B. 0
C. 2
D. 3
E. 4

Answer 1

Option a: -1

Option b: 0

Step-by-step explanation:

The function
`f(x)=-2 x+2` and
`g(x)=\left((1)/(3)\right)^(x)+1`

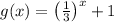
To determine the solution of
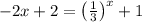`-2 x+2=\left((1)/(3)\right)^(x)+1` and solving the expression using lambert's form, we get the solution
`x=-1, x=0`

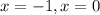
Hence, the solution to the functions
`f(x)=-2 x+2` and
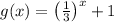`g(x)=\left((1)/(3)\right)^(x)+1` are -1 and 0.

Also, by looking at the graph, we can see that, the graphs f(x) and g(x) intersect at the points
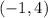`(-1,4)` and
`(0,2)`.

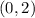Hence, the solution to
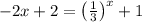`-2 x+2=\left((1)/(3)\right)^(x)+1` is -1 and0.

Thus, Option a and Option b are the correct answers.