Answer:
The time for the second train to catch up with the first train = T₂
T₂ =
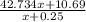 where x is the time it takes for each refueling, hence when x = 5 minutes then the second train meets up wirh the first train in 42.75 Hrs or at 3:45 a.m. on the next two days
where x is the time it takes for each refueling, hence when x = 5 minutes then the second train meets up wirh the first train in 42.75 Hrs or at 3:45 a.m. on the next two days
Explanation:
Velocity of first train = 39.1 miles per hour
Velocity of second train = 45.5 miles per hour
Time of depature of the first train = 12 pm
Time of depature of the secon train = 7 pm
Refueling = every 15 minutes
Therefore
From the formula for velocity we have, velocity = Displacement/ time
Therefore Displacement =Velocity × time
If the refueling time = x seconds then total time for each train = T₁ + 4·x·T₁
Where T is the total time hence
v₁ × (T₁ + 4·x·T₁) = v₂ × (T₂ + 4·x·T₂)
However the first train is ahead by 7 hours hence
v₁ × (T₁ + 4·x·T₁ + 7) = v₂ × (T₂ + 4·x·T₂)
or 39.1×(T₁ + 4·x·T₁ + 7) = 45.5×(T₂ + 4·x·T₂)
That is T₁ = T₂ +7
hence 39.1×(T₂ +7 + 4·x·(T₂ +7)) = 45.5×(T₂ + 4·x·T₂)
= 39.1×((4·x+1)×T₂+28×x+7) = 45.5×(T₂ + 4·x·T₂)
Therefore T₂ =
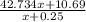 Hence if they stop for 5 minutes which is equal to 5/60 of 1 hour or 1/12 hour we have
Hence if they stop for 5 minutes which is equal to 5/60 of 1 hour or 1/12 hour we have
T₂ = 42.75 Hrs or since there are 24 hours in a day we have
1 day 8 3/4 hours or 3:45 a.m. on the next two days