Question

A train is moving at 39.1 miles per hour. Another train is moving at 45.5 miles per hour. Both trains are to stop at a designated area. The first train at 12pm, the latter 7pm. If the trains must both stop for fuel every 15 minutes, at what time will they cross paths?

Answer 1

The time for the second train to catch up with the first train = T₂

T₂ =
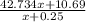`(42.734x + 10.69)/(x+0.25)` where x is the time it takes for each refueling, hence when x = 5 minutes then the second train meets up wirh the first train in 42.75 Hrs or at 3:45 a.m. on the next two days

Explanation:

Velocity of first train = 39.1 miles per hour

Velocity of second train = 45.5 miles per hour

Time of depature of the first train = 12 pm

Time of depature of the secon train = 7 pm

Refueling = every 15 minutes

Therefore

From the formula for velocity we have, velocity = Displacement/ time

Therefore Displacement =Velocity × time

If the refueling time = x seconds then total time for each train = T₁ + 4·x·T₁

Where T is the total time hence

v₁ × (T₁ + 4·x·T₁) = v₂ × (T₂ + 4·x·T₂)

However the first train is ahead by 7 hours hence

v₁ × (T₁ + 4·x·T₁ + 7) = v₂ × (T₂ + 4·x·T₂)

or 39.1×(T₁ + 4·x·T₁ + 7) = 45.5×(T₂ + 4·x·T₂)

That is T₁ = T₂ +7

hence 39.1×(T₂ +7 + 4·x·(T₂ +7)) = 45.5×(T₂ + 4·x·T₂)

= 39.1×((4·x+1)×T₂+28×x+7) = 45.5×(T₂ + 4·x·T₂)

Therefore T₂ =
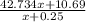`(42.734x + 10.69)/(x+0.25)` Hence if they stop for 5 minutes which is equal to 5/60 of 1 hour or 1/12 hour we have

T₂ = 42.75 Hrs or since there are 24 hours in a day we have

1 day 8 3/4 hours or 3:45 a.m. on the next two days