Question

Consider the graph of quadrilateral ABCD, what is the most specific name for quadrilateral ABCD ?

Answer 1

The missing figure is attached down

Answer:

The most specific name for quadrilateral ABCD is parallelogram

Explanation:

The quadrilateral is a parallelogram if

• Its two diagonals bisect each other
• Its two diagonals not equal in length
• Its two diagonals not perpendicular

From the attached figure

∵ The diagonals of the quadrilateral are AC and BD

∵ A = (-2 , 3) , C = (0 , -3)

- Find the slope of AC and its length using the rule of the slope

and the rule of the distance

∵
`m_(AC)=(-3-3)/(0--2)`

∴
`m_(AC)=(-6)/(2)=-3`

∵
`d_(AC)=\sqrt{(0--2)^(2)+(-3-3)^(2)}=\sqrt{(2)^(2)+(-6)^(2)}`

∴
`d_(AC)=√(4+36)=√(40)`

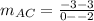
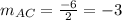
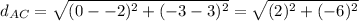
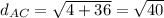
- Find the mid-point of AC

∵
`M_(AC)=((-2+0)/(2),(3+-3)/(2))`

∴
`M_(AC)=(-1,0)`

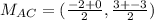
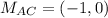
∵ B = (2 , 2) , C = (-4 , -2)

- Find the slope of AC and its length using the rule of the slope

and the rule of the distance

∵
`m_(BD)=(-2-2)/(-4-2)`

∴
`m_(BD)=(-4)/(-6)=(2)/(3)`

∵
`d_(BD)=\sqrt{(-4-2)^(2)+(-2-2)^(2)}=\sqrt{(-6)^(2)+(-4)^(2)}`

∴
`d_(BD)=√(36+16)=√(52)`

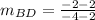
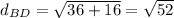
- Find the mid-point of AC

∵
`M_(BD)=((2+-4)/(2),(2+-2)/(2))`

∴
`M_(BD)=(-1,0)`

∵
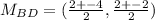
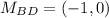
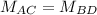`M_(AC)=M_(BD)` ⇒ diagonals bisect each other

∵
`d_(AC)` ≠
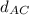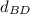`d_(BD)` ⇒ diagonals not equal in length

∵ The product of their slopes = -3 ×
`(2)/(3)` = -2

∵ The product of the slopes of the perpendicular lines is -1

∴ AC and BD are not perpendicular

∴ ABCD is a parallelogram

The most specific name for quadrilateral ABCD is parallelogram