Question

Vector A has magnitude 8.00 mm and is in the xy-plane at an angle of 127∘ counterclockwise from the +x–axis (37∘ past the +y-axis). The sum A +B is in the −y-direction and has magnitude 12.0 mm. Find the vector B.

Answer 1

-75.35°

Step-by-step explanation:

Let C be the sum of the two vectors A and B. Hence, we can write the following

`A_(x) +B_(x) =C_(x) ......(1)\\A_(y) +B_(y) =C_(y) ......(2)`

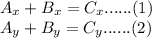
but since the vector C is in the -y direction,
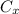`C_(x)` = 0 and
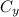`C_(y)` = —12 m.

Thus

`B_(x) =-A_(x) =-[-Acos(180-127)]=(8)*cos(53)\\B_(x) =4.81m`

similarly, we can determine
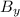`B_(y)` by rearranging equation (1)

`B_(y) =C_(y) -A_(y) =-12m-[(8)*sin(53)\\B_(y) =-18.4m`

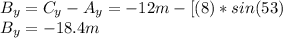
so the magnitude of B is

`B=\sqrt{B_(x)^2+B_(y)^2 } \\B=19m`

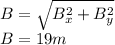
Finally, the direction of B can be calculated as follows

Ф=
`tan^(-1) ((B_(y) )/(B_(x) ) )\\=-75.35`

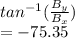
hence the vector B makes an angle of 75.35 clockwise with + x axis