Answer:
-75.35°
Step-by-step explanation:
Let C be the sum of the two vectors A and B. Hence, we can write the following
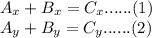
but since the vector C is in the -y direction,
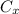 = 0 and
= 0 and
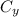 = —12 m.
= —12 m.
Thus
![B_(x) =-A_(x) =-[-Acos(180-127)]=(8)*cos(53)\\B_(x) =4.81m](https://img.qammunity.org/2021/formulas/physics/college/zon3bnh2qdr4jk8qzn5ghz2xl5wgk1was1.png)
similarly, we can determine
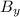 by rearranging equation (1)
by rearranging equation (1)
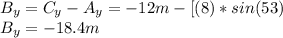
so the magnitude of B is
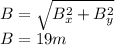
Finally, the direction of B can be calculated as follows
Ф=
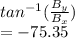
hence the vector B makes an angle of 75.35 clockwise with + x axis