Question

The driver of a car wishes to pass a truck that is traveling at a constant speed of 20.0 m/s (about 45 mi/h). Initially, the car is also traveling at 20.0 m/s, and its front bumper is 24.0 m behind the truck’s rear bumper. The car accelerates at a constant 0.600m/s^2, then pulls back into the truck’s lane when the rear of the car is 26.0 m ahead of the front of the truck. The car is 4.5 m long, and the truck is 21.0 m long. (a) How much time is required for the car to pass the truck? (b) What distance does the car travel during this time? (c) What is the final speed of the car?

Answer 1

15.8640053791 s

392.780107582 m

29.5184032275 m/s

Step-by-step explanation:

0 denotes initial

x denotes displacement

c denotes car

t denotes truck

r denotes rear

`x_0_(cr)=-49.5\ m`

`a_c=0.6\ m/s^2`

`x_0_(t)=0`

`v_0_(c)=v_0_(t)`

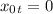
For the car

`x_c=x_0+v_0_(c)t+(1)/(2)at^2`

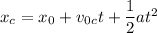
The displacement of the truck will be

`x_t=v_tt`

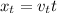
From the above two equations we get

`x_c-x_t=x_0+v_0_(c)+(1)/(2)at-v_(t)t=26\\\Rightarrow 26=x_0+(1)/(2)at^2\\\Rightarrow 26+49.5=(1)/(2)0.6t^2\\\Rightarrow t=\sqrt{(2(26+49.5))/(0.6)}\\\Rightarrow t=15.8640053791\ s`

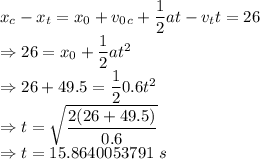
The time taken is 15.8640053791 s

`x-x_0=v_(0)_(c)t+(1)/(2)at^2\\\Rightarrow x-x_0=20* 15.8640053791+(1)/(2)0.6* 15.8640053791^2\\\Rightarrow x-x_0=392.780107582\ m`

The distance the car travels is 392.780107582 m

`v=v_0+at\\\Rightarrow v=20+0.6* 15.8640053791\\\Rightarrow v=29.5184032275\ m/s`

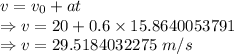
The velocity of the car is 29.5184032275 m/s