Answer:
15.8640053791 s
392.780107582 m
29.5184032275 m/s
Step-by-step explanation:
0 denotes initial
x denotes displacement
c denotes car
t denotes truck
r denotes rear

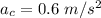
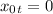
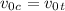
For the car
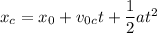
The displacement of the truck will be
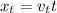
From the above two equations we get
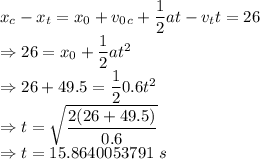
The time taken is 15.8640053791 s

The distance the car travels is 392.780107582 m
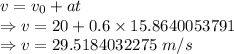
The velocity of the car is 29.5184032275 m/s