Answer:
- Equilibrium quantity: 7 units
Step-by-step explanation:
This is an example of the using algebraic solution of simultaneous linear equations in demand and supply analysis.
The equation for the price, P, for the supply of Qs units is:

And the equation for the price, P, for the demand of Qd units is:

In the equilibrium, the quantity demanded, Qd, and the quantity supplied, Qs are equal.
Call Qe the equilibrium quantity. Then, you can solve for Qs = Qd = Qe.
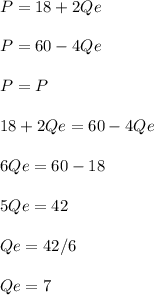
Thus, the equilibrium quantity is 7.
Substitue Qs = 7 or Qd = 7 in the corresponding equation for the price to find the equlibrium price:
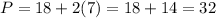
Assming the currency is dollars, it is $32.