Question

The functions underlying the example in the table are linear and can be presented

as P = 18+2Qs and P = 60−4Qd. Solve the two equations for the equilibrium
price and quantity values.

Answer 1

• Equilibrium price: $ 32

• Equilibrium quantity: 7 units

Step-by-step explanation:

This is an example of the using algebraic solution of simultaneous linear equations in demand and supply analysis.

The equation for the price, P, for the supply of Qs units is:

`P=18+2Qs`

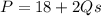
And the equation for the price, P, for the demand of Qd units is:

`P=60-4Qd`

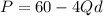
In the equilibrium, the quantity demanded, Qd, and the quantity supplied, Qs are equal.

Call Qe the equilibrium quantity. Then, you can solve for Qs = Qd = Qe.

`P=18+2Qe\\ \\ P=60-4Qe\\ \\ P=P\\ \\ 18+2Qe=60-4Qe\\ \\ 6Qe=60-18\\ \\ 5Qe=42\\ \\Qe=42/6\\ \\ Qe=7`

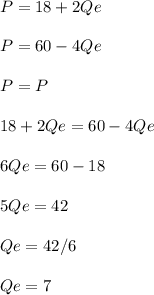
Thus, the equilibrium quantity is 7.

Substitue Qs = 7 or Qd = 7 in the corresponding equation for the price to find the equlibrium price:

`P=18+2(7)=18+14=32`

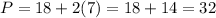
Assming the currency is dollars, it is $32.