Question

Help meeeeeeeeeeeeeeeeeeeeeee

Answer 1

Option B:

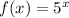`f(x)=5^(x)` is increasing function.

Solution:

A function is increasing when the f(x) value increases as x-value increases.

Option A:
`f(x)=\left((1)/(15)\right)^(x)`

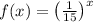
Substitute x = 1 and x = 2 in f(x).

`f(1)=\left((1)/(15)\right)^(1)=0.0666`

`f(2)=\left((1)/(15)\right)^(2)=0.0044`

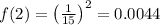
0.0666 > 0.0044

Here x is increasing but f(x) is decreasing.

So, the function is not increasing.

Option B:
`f(x)=5^(x)`

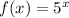
Substitute x = 1 and x = 2 in f(x).

`f(1)=5^(1)=5`

`f(2)=5^(2)=25`

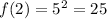
5 < 25

Here f(x) is increasing as x is increasing.

So, the function is increasing.

Option C:
`f(x)=\left((1)/(5)\right)^(x)`

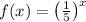
Substitute x = 1 and x = 2 in f(x).

`f(1)=\left((1)/(5)\right)^(1)=0.2`

`f(2)=\left((1)/(5)\right)^(2)=0.04`

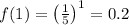
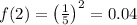
0.2 > 0.04

Here x is increasing but f(x) is decreasing.

So, the function is not increasing.

Option D:
`f(x)=(0.5)^(x)`

`f(1)=(0.5)^(1)=0.5`

`f(2)=(0.5)^(2)=0.25`

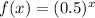
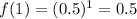
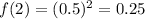
0.5 > 0.25

Here x is increasing but f(x) is decreasing.

So, the function is not increasing.

Option B is the correct answer.

Hence
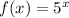`f(x)=5^(x)` is increasing function.