Question

The side lengths of the base of a triangular prism are 5 meters, 8 meters, and 10 meters

The height of the prism is 16.5 meters.
What is the lateral surface area of the prism in square meters?

Answer 1

379.5

Step-by-step explanation:

Answer 2

The lateral surface area of the triangular prism is
`379.5 sq.units`

Step-by-step explanation:

The side lengths of the base of the triangular prism are 5 meters, 8 meters, and 10 meters.

It is given that the height of the prism is 16.5 meters.

To determine the lateral surface area of the prism, let us use the formula
`LSA=(a+b+c) h`

where a, b,c are the side lengths of the base of the triangular prism and h is the height of the prism.

Here
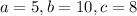`a=5, b=10, c=8` and
`h=16.5`

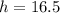
Substituting these values in the formula, we have,

`LSA=(5+10+8)16.5`

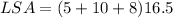
Simplifying, we get,

`LSA=(23)16.5`

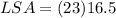
Multiplying, we get,

`LSA=379.5`

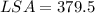
Thus, the lateral surface area of the triangular prism is
`379.5 sq.units`