Answer:
 is the drop in the water temperature.
is the drop in the water temperature.
Step-by-step explanation:
Given:
- mass of ice,
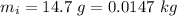
- mass of water,

Assuming the initial temperature of the ice to be 0° C.
Apply the conservation of energy:
- Heat absorbed by the ice for melting is equal to the heat lost from water to melt ice.
Now from the heat equation:
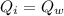
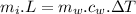 ......................(1)
......................(1)
where:
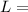 latent heat of fusion of ice
latent heat of fusion of ice
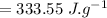
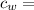 specific heat of water
specific heat of water
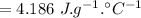
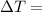 change in temperature
change in temperature
Putting values in eq. (1):
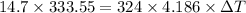
 is the drop in the water temperature.
is the drop in the water temperature.