Question

A plane wall of thickness 0.1 m and thermal conductivity 25 W/m·K having uniform volumetric heat generation of 0.3 MW/m3 is insulated on one side, while the other side is exposed to a fluid at 32°C. The convection heat transfer coefficient between the wall and the fluid is 400 W/m2·K. Determine the maximum temperature in the wall.

Answer 1

T = 167 ° C

Step-by-step explanation:

To solve the question we have the following known variables

Type of surface = plane wall ,

Thermal conductivity k = 25.0 W/m·K,

Thickness L = 0.1 m,

Heat generation rate q' = 0.300 MW/m³,

Heat transfer coefficient hc = 400 W/m² ·K,

Ambient temperature T∞ = 32.0 °C

We are to determine the maximum temperature in the wall

Assumptions for the calculation are as follows

• Negligible heat loss through the insulation
• Steady state system
• One dimensional conduction across the wall

Therefore by the one dimensional conduction equation we have

`k(d^(2)T )/(dx^(2) ) +q'_(G) = \rho c(dT)/(dt)`

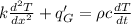
During steady state

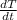`(dT)/(dt)` = 0 which gives
`k(d^(2)T )/(dx^(2) ) +q'_(G) = 0`

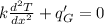
From which we have
`(d^(2)T )/(dx^(2) ) = -(q'_(G))/(k)`

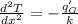
Considering the boundary condition at x =0 where there is no heat loss

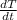`(dT)/(dt)` = 0 also at the other end of the plane wall we have

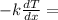`-k(dT )/(dx ) =` hc (T - T∞) at point x = L

Integrating the equation we have

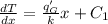`(dT )/(dx ) = (q'_(G))/(k) x+ C_(1)` from which C₁ is evaluated from the first boundary condition thus

0 =
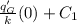`(q'_(G))/(k) (0)+ C_(1)` from which C₁ = 0

From the second integration we have

`T = -(q'_(G))/(2k) x^(2) + C_(2)`

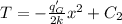
From which we can solve for C₂ by substituting the T and the first derivative into the second boundary condition s follows

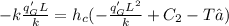`-k(q'_(G)L)/(k) = h_(c)( -(q'_(G)L^(2) )/(k) + C_(2)-T∞)` → C₂ =
`q'_(G)L((1)/(h_(c) )+ (L)/(2k) } )+T∞`

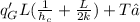
T(x) =
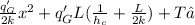`(q'_(G))/(2k) x^(2) + q'_(G)L((1)/(h_(c) )+ (L)/(2k) } )+T∞` and T(x) = T∞ +
`(q'_(G))/(2k) (L^(2)+((2kL)/(h_(c) )} )-x^(2) )`

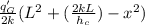
∴ Tmax → when x = 0 = T∞ +
`(q'_(G))/(2k) (L^(2)+((2kL)/(h_(c) )} ))`

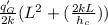
Substituting the values we get

T = 167 ° C