Answer:
The two results were 35 hours and 1.25 hours, approximately one hour fifteen minutes. Although both times meet the condition, the response of choosing one or the other time will depend on the growth behavior of P. aeruginosa
Step-by-step explanation:
To determine the time(s) in which the population was 100000, you must solve the quadratic equation, clearing t, as follows:
P=-1600t^2+58000t+30000=100000
Sorting the equation and equalizing zero:
1600t^2-58000t+70000=0
a b c
applying the quadratic equation is:

This equation has two solutions:

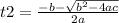
replacing the values in both equations, we have:
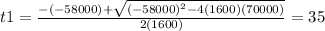
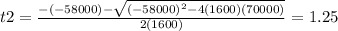
The two results were 35 hours and 1.25 hours, approximately one hour fifteen minutes. Although both times meet the condition, the response of choosing one or the other time will depend on the growth behavior of P. aeruginosa