Question

A two-story hotel has interior columns for the rooms that are spaced 6 m apart in two perpendicular directions. Determine the reduced live load supported by a typical interior column on the first floor under the public rooms.

Answer 1

3021.7 N/m^2 or 3.022 kN/m^2

Step-by-step explanation:

The area of the interior column is equivalent to 6*6 = 36 m^2. The length
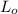`L_(o)` of the structure is 4790 N/m^2. The live load element factor (
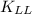`K_(LL)`) is 4. The reduced live load will be:

L =
`L_(o)(0.25 + \frac{4.57}{\sqrt{K_(LL)A_(T)}})` =
`= 4790(0.25 + (4.57)/(√(4*36))) = 4790(0.25 + (4.57)/(√(144))) = 4790(0.25 + (4.57)/(12)) = 4790(0.25 + 0.381) = 3021.7`

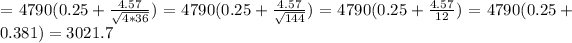
Therefore, the value of the reduced live load that will be supported by the column is 3021.7 N/m^2 or 3.022 kN/m^2.

This is less than 0.4*
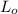`L_(o)` = 0.4*4790 = 1916 N/m^2