Question

The size 4 soccer ball Sean’s team uses should weigh no more than 0.37 kilograms, and no less than 0.31 kilograms. A soccer bag has two balls in it. What is the most they could weigh together? The least?

Answer 1

Answers:

Q: What is the most they could weigh together?

A: 0.74 kg

-----

Q: What is the least they could weigh together?

A: 0.62 kg

=================================================

Work Shown:

x = weight of first ball

y = weight of second ball

each ball has a weight range of 0.31 kg to 0.37 kg, so,

`0.31 \le x \le 0.37`

`0.31 \le y \le 0.37`

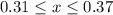
add straight down to get

`0.31+0.31 \le x+y \le 0.37+0.37`

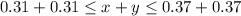
which simplifies to

`0.62 \le x+y \le 0.74`

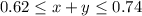
the two soccer balls have a weight range of 0.62 to 0.74, inclusive of both endpoints.

--------

Without using algebra, you basically just add the smallest the two weights could be (0.31) to itself to get 0.31+0.31 = 0.62 which represents the smallest the two weights combined can be. The same happens with the largest weight of 0.37 to get 0.37+0.37 = 0.74 as the max weight of both objects together.