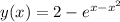Question

Consider the differential equation:

dy/dx + 2xy = y + 4x − 2
(a) Classify this equation by:
i. order
ii. linear or nonlinear
iii. separable or nonseparable
(b) Find the general solution of this differential equation. Specify the largest interval I on which the solution is defined.
(c) Verify that your solution is correct by plugging it back into the differential equation.
(d) In part (b), you should have found a one-parameter family of solutions. Find a solution that satisfies the initial condition y(0) = 1.

Answer 1

(a) First order linear separable differential equation

(b)

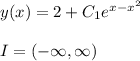
`y(x)=2+C_1e^(x-x^2) \\\\I=(-\infty,\infty)`

(c)

(d)

`y(x)=2-e^(x-x^2)`

Explanation:

(b) Solve for
`(dy)/(dx)`

`(dy)/(dx)=4x+y-2xy-2\\ \\Simplify\\\\(dy)/(dx)=(2x-1)(2-y)\\\\Divide\hspace{3}both\hspace{3}sides\hspace{3}by\hspace{3}2-y\hspace{3}and\hspace{3}multiply\hspace{3}both\hspace{3}sides\hspace{3}by\hspace{3}dx\\\\(dy)/(2-y)=(2x-1) dx\\\\Integrate\hspace{3}both\hspace{3}sides\\\\\int(dy)/(2-y) \, =\int\ (2x-1) dx\\\\Evaluate\hspace{3}the\hspace{3}integrals\\\\-log(2-y)=x^2-x+C_1\\\\Solving\hspace{3}for\hspace{3}y\\\\y=2+C_1e^(x-x^2)`

The domain of y is:
`x\in R\hspace{3}or\hspace{3}(-\infty,\infty)`

So the lasrgest interval I on which the solution is defined is:

`I=(-\infty,\infty)`

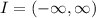
(c)

Differentiate y:

`(dy)/(dx)=C_1(1-2x)e^(x-x^2) =C_1e^(x-x^2)-2xC_1e^(x-x^2)`

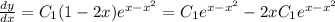
Evaluate this result into the differential equation:

`(dy)/(dx)=4x+y-2xy-2\\\\C_1e^(x-x^2) -2xC_1e^(x-x^2) =4x+2+C_1e^(x-x^2)-4x-2xC_1e^(x-x^2)-2\\\\C_1e^(x-x^2) -2xC_1e^(x-x^2) =C_1e^(x-x^2) -2xC_1e^(x-x^2)`

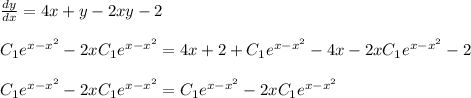
Therefore, the solution is correct.

(d)

Simply evaluate the function y for x=0 and solve for C1:

`y(0)=2+C_1e^(0-0^2) =1\\\\2+C_1e^0=1\\\\2+C_1*1=1\\\\2+C_1=1\\\\C_1=-1`

Finally substitute into y:

`y(x)=2-e^(x-x^2)`