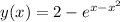Answer:
(a) First order linear separable differential equation
(b)
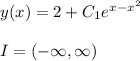
(c)
(d)
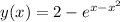
Explanation:
(b) Solve for
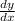

The domain of y is:
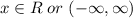
So the lasrgest interval I on which the solution is defined is:
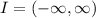
(c)
Differentiate y:
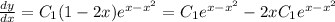
Evaluate this result into the differential equation:
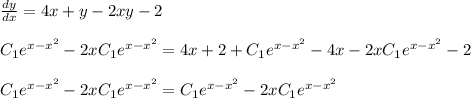
Therefore, the solution is correct.
(d)
Simply evaluate the function y for x=0 and solve for C1:
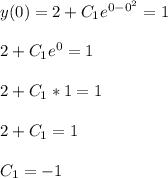
Finally substitute into y: