A.
mu = population mean = advertised mean = 23
x = raw score = 19.4
sigma = population standard deviation = 1.07
z = (x - mu)/sigma
z = (19.4 - 23)/1.07
z = -3.36448598130841
z = -3.36
=======================================
B.
The general rule is that if
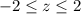 , then the z score is not unusual. Otherwise, it is unusual.
, then the z score is not unusual. Otherwise, it is unusual.
Since z = -3.36 falls outside the range, the car is getting unusually low gas mileage.