Question

Suppose you buy a new car whose advertised mileage is 23 miles per gallon​ (mpg). After driving your car for several​ months, you find that its mileage is 19.4 mpg. You telephone the manufacturer and learn that the standard deviation of gas mileages for all cars of the model you bought is 1.07 mpg.

A. Find the​ z-score for the gas mileage of your​ car, assuming the advertised claim is correct.
B. Does it appear that your car is getting unusually low gas​mileage?

Answer 1

A.

mu = population mean = advertised mean = 23

x = raw score = 19.4

sigma = population standard deviation = 1.07

z = (x - mu)/sigma

z = (19.4 - 23)/1.07

z = -3.36448598130841

z = -3.36

=======================================

B.

The general rule is that if
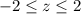`-2 \le z \le 2`, then the z score is not unusual. Otherwise, it is unusual.

Since z = -3.36 falls outside the range, the car is getting unusually low gas mileage.

Answer 2

B.

Explanation: