Question

A satellite is in a circular orbit 21000 km above the Earth’s surface; i.e., it moves on a circular path under the influence of nothing but the Earth’s gravity. Find the speed of the satellite. The radius of the Earth is 6.37 × 106 m, and the acceleration of gravity at the satellite’s altitude is 0.532655 m/s 2. Find the time it takes to complete one orbit around the Earth.

Answer 1

(orbital speed of the satellite) V₀ = 3.818 km

Time (t) = 4.5 × 10⁴s

Step-by-step explanation:

Given that:

The radius of the Earth is 6.37 × 10⁶ m; &

the acceleration of gravity at the satellite’s altitude is 0.532655 m/s

We can calculate the orbital speed of the satellite by using the formula:

Orbital Speed (V₀) = √(r × g)

radius of the orbit (r) = 21000 km + 6.37 × 10⁶ m

= (2.1 × 10⁷ + 6.37 × 10⁶) m

= 27370000

= 2.737 × 10⁷m

Orbital Speed (V₀) = √(r × g)

Orbital Speed (V₀) = √(2.737 × 10⁷ × 0.532655 )

= 3818.215

= 3.818 × 10³

= 3.818 Km

To find the time it takes to complete one orbit around the Earth; we use the formula:

Time (t) = 2 π ×
`(r)/(V_o)`

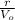
= 2 × 3.14 ×
`(2.737*10^7)/(3.818*10^3)`

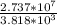
= 45019.28

= 4.5 × 10 ⁴ s