Question

A dog running in an open field has components of velocity vx= 2.8 m/s and vy= -2.3 m/s at time t1= 10.3s . For the time interval from t1= 10.3 to t2= 22.7 , the average acceleration of the dog has magnitude 0.43 m/s2 and direction 33.5 degree measured from the +x-axis toward the +y-axis .

A) At time t2= 22.7s , what are the x- and y-components of the dog's velocity?
B) What is the magnitude of the dog's velocity?
C) What is the direction of the dog's velocity (measured from the +x-axis toward the +y-axis... (answer in θ)

Answer 1

A) At t2 = 22.7 s, the x-component of the velocity is 7.3 m/s and the y-component is 0.7 m/s.

B) The magnitude of the dog's velocity is 7.3 m/s.

C) The direction of the velocity vector is 5.5° from the x-axis to the y-axis.

Step-by-step explanation:

Hi there!

The components of the velocity vector can be calculated using this equations:

vx = v0x + ax · t

vy = v0y + ay · t

Where:

vx = x-component of the velocity

v0x = initial x-component of the velocity.

ax = x-component of the acceleration.

vy = y-component of the velocity.

v0y = initial y-component of the velocity.

ay = y-component of the acceleration.

t = time

A) Let's calculate the velocity using the equations. The initial velocity vector is v0 = (2.8, -2.3) m/s. The elapsed time is (22.7 s - 10.3 s) 12.4 s.

To calculate the components of the acceleration vector, we use trigonometry:

cos θ = ax/a (where "a" is the magnitude of the acceleration)

ax = a · cos θ

ax = 0.43 m/s² · cos(33.5°) = 0.36 m/s²

ay = a · sin θ

ay = 0.43 m/s² · sin(33.5°) = 0.24 m/s²

Now, we can calculate the velocity:

vx = v0x + ax · t

vx = 2.8 m/s + 0.36 m/s² · 12.4 s

vx = 7.3 m/s

vy = v0y + ay · t

vy = -2.3 m/s + 0.24 m/s² · 12.4 s

vy = 0.7 m/s

At t2 = 22.7 s, the x-component of the velocity is 7.3 m/s and the y-component is 0.7 m/s.

b) The magnitude of the velocity is calculated as follows:

`|v| = \sqrt{(vx)^(2) + (vy)^(2)} \\|v| = \sqrt{(7.3 m/s)^(2) + (0.7 m/s)^(2)} = 7.3 m/s`

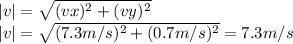
The magnitude of the dog's velocity is 7.3 m/s

c) Now that we have the magnitude of the velocity, we can calculate its direction:

sin θ = vy / v

sin θ = 0.7 m/s / 7.3 m/s

θ = 5.5°

The direction of the velocity vector is 5.5° from the x-axis to the y-axis.