Question

The Pi Mu Epsilon mathematics honorary society of Outstanding Universitywishes to have a picture taken of its six officers. There will be two rowsof three people. How many different way can the six officers be arranged?

Answer 1

720

Explanation:

I will use the following counting principle:

Product rule: if there are n ways of doing something, and m ways of doing another thing, there are n×m ways of doing both things.

First, we have to choose the 3 people that will be in the first row. This is a 3-element subset of the set of six people, therefore there are
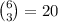`\binom{6}{3}=20` ways of doing this.

Now, we have to arrange the order of the 2 lrows. Each one has 3 people, so there are 3!=6 ways to form one rows. Hence, there are 3!²=36 ways of arranging the two rows.

By the product rule, there are 20×36=720 ways of arrange the officers.