Answer:
a)
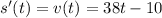
b)
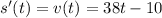
We just need to replace the different values of t and see what we got:
t=0,

t =5,
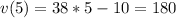
t=8,

Explanation:
Assuming this complete question: "If a function s (t )gives the position of a function at time t, the derivative gives the velocity, that is, v (t)=s'(t ). For the given position function, find (a) v(t) and (b) the velocity when t=0, t=5, and t=8.
"
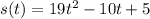
Part a
The velocity is defined as

And if we derivate the position we got:
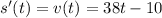
Part b
Since we have the function for the velocity:
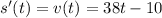
We just need to replace the different values of t and see what we got:
t=0,

t =5,
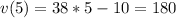
t=8,
