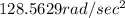Answer:
(A) Tangential speed will be equal to 7.09 m/sec
(B) Radial acceleration will be equal to
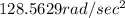
Step-by-step explanation:
We have given angular speed of the wheel
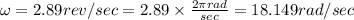
Radius of the track r = 39.1 cm = 0.391 m
(A) Tangential speed will be equal to
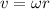 , here
, here
 is angular speed and r is radius
is angular speed and r is radius
So tangential speed
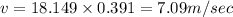
So tangential speed will be equal to 7.09 m/sec
(B) Radial acceleration will be equal to
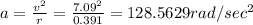
So radial acceleration will be equal to