Answer with Step-by-step explanation:
We are given that
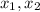 and
and
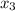 are linearly independent.
are linearly independent.
By definition of linear independent there exits three scalar
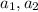 and
and
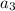 such that
such that
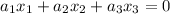
Where
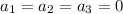
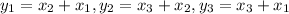
We have to prove that
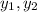 and
and
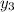 are linearly independent.
are linearly independent.
Let
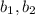 and
and
 such that
such that
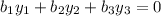
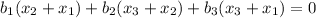
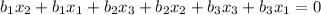
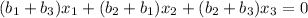
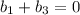
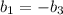 ...(1)
...(1)
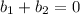
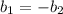 ..(2)
..(2)

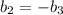 ..(3)
..(3)
Because
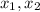 and
and
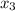 are linearly independent.
are linearly independent.
From equation (1) and (3)
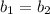 ...(4)
...(4)
Adding equation (2) and (4)
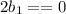

From equation (1) and (2)
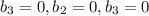
Hence,
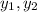 and
and
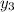 area linearly independent.
area linearly independent.