Answer:
- 97.5% of the students have grade point averages that are at least 3.4
Step-by-step explanation:
1. Find how many standard deviations is 3.4 from the mean, 2.62
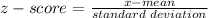
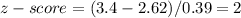
2. Apply the empirical rule
The empirical rule, or 68 - 95 - 99.7 rule, states that, for a normal distribution (a bell-shaped distribution), 68% of the data are within one standar deviation of the mean, 95% of the data are within two standard deviations from the mean, and 99.7% of the data are within three standard deviations from the mean.
We calculated that 3.4 is 2 standard deviations from the mean.
Since 95% of the data are within 2 standard deviations from the mean, 5% of the data are out of the 2 standard deviations region; half of that (2.5%) are abovethe mean + 2 standard deviations
Hence, the grade point averages of 95% + 2.5% of the students are below the mean plus two standard deviations, and you can say that that is the percentage of students whose grade point averages are at least 3.4.