The area of dilated rectangle is 40 square feet
Solution:
Given that,
A rectangle with an area of 5/8 ft squared is dilated by a factor of 8
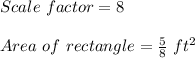
If two figures are similar, then the ratio of its areas is equal to scale factor squared
Let,
z = the scale factor
x = the area of the dilated rectangle
y = the area of the original rectangle
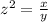
From given,
z = 8
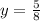
Therefore,
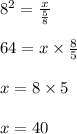
Thus the area of dilated rectangle is 40 square feet