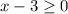The inequality
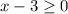 can be used to find the domain of
can be used to find the domain of
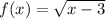
Answer: Option B
Explanation:
We have
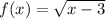 , domain is the set of all possible x-values which will make the function "work", and will output real y-values. Basically to find domain of any function means to find range of values of x that will give real values of y.
, domain is the set of all possible x-values which will make the function "work", and will output real y-values. Basically to find domain of any function means to find range of values of x that will give real values of y.
For the equation
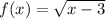 , we know that there's no value ( iota or complex numbers are there but here we will deal with real numbers ) of negative numbers under square root
, we know that there's no value ( iota or complex numbers are there but here we will deal with real numbers ) of negative numbers under square root
∴
 must be greater than or equal to 0.
must be greater than or equal to 0.
⇒