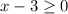Question

If f (x) = StartRoot x minus 3 EndRoot, which inequality 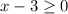can be used to find the domain of f(x)? Options Below

A. StartRoot x minus 3 EndRoot greater-than-or-equal-to 0
B. x minus 3 greater-than-or-equal-to 0
C. StartRoot x minus 3 EndRoot less-than-or-equal-to 0
D. x minus 3 less-than-or-equal-to 0

Answer 1

B

Explanation:

Answer 2

The inequality
`x-3 \geq 0` can be used to find the domain of
`f(x)=√(x-3)`

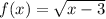
Answer: Option B

Explanation:

We have
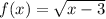`f(x)=√(x-3)`, domain is the set of all possible x-values which will make the function "work", and will output real y-values. Basically to find domain of any function means to find range of values of x that will give real values of y.

For the equation
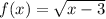`f(x)=√(x-3)` , we know that there's no value ( iota or complex numbers are there but here we will deal with real numbers ) of negative numbers under square root

∴
`{(} x-3 {)}` must be greater than or equal to 0.

⇒
`x-3 \geq 0`