Question

How do you do this question? Step by step please

Answer 1

6

Explanation:

A right Riemann sum approximates a definite integral as:

`\int\limits^b_a {f(x)} \, dx \approx \sum\limits_(k=1)^(n)f(x_(k)) \Delta x \\where\ \Delta x = (b-a)/(n) \ and\ x_(k)=a+\Delta x * k`

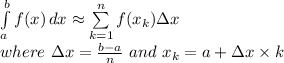
The exact value of the definite integral can be found by taking the limit of the Riemann sum as n approaches infinity:

`\int\limits^b_a {f(x)} \, dx = \lim_(n \to \infty) \sum\limits_(k=1)^(n)f(x_(k)) \Delta x \\where\ \Delta x = (b-a)/(n) \ and\ x_(k)=a+\Delta x * k`

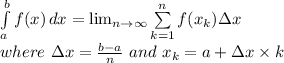
Given that the sum is equal to 2 (n + 1) (3n + 2) / n², the exact value of the integral is:

lim(n→∞) 2 (n + 1) (3n + 2) / n²

lim(n→∞) 2 (3n² + 5n + 2) / n²

lim(n→∞) (6n² + 10n + 4) / n²

6