Answer:
a = 0.05
b = 0.028
c =0.014
Explanation:
Given that;
inspector A visually inspected 1000 ceramic mugs and found flaws in 36 of them.
Let X represent Inspector A
P(X) =
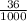
= 0.036
inspector B visually inspected 1000 ceramic mugs and found flaws in 42 of them.
Let Y represent Inspector B
P(Y) =
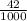
= 0.042
A total of 950 mugs were found to be good by both inspectors.
i.e (X∩Y)' = 950
P (X∩Y)' =
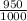
= 0.095
We are tasked to find :
a) the probability that a flaw was found in this mug by at least one of the two inspectors [i.e P (X∪Y)]
b) the probability that flaws were found in this mug by both inspectors.
[i.e P ( X∩Y)]
c) the probability that a flaw was found by inspector B but not by inspector A. [i.e P (X) - P ( X∩Y)]
With a);
P (X∪Y) = 1 - P(A∩B)'
P (X∪Y) = 1 - 0.950
P (X∪Y) = 0.05
b)
P(X∩Y) = P(X) + P(Y) - P(X∪Y)
P(X∩Y) = 0.036 + 0.042 + 0.05
P(X∩Y) = 0.028
c)
P (X) - P ( X∩Y) = 0.042 - 0.028
P (X) - P ( X∩Y) = 0.014
Therefore;
the probability that a flaw was found in this mug by at least one of the two inspectors = 0.05
the probability that flaws were found in this mug by both inspectors = 0.028; &
the probability that a flaw was found by inspector B but not by inspector A = 0.014