Question

A police officer in a patrol car parked in a 70 km/h speed zone observes a passing automobile traveling at a slow, constant speed. Believing that the driver of the automobile might be intoxicated, the office starts his car, accelerates uniformly to 90 km/h in 8 s, and, maintaining a constant velocity of 90 km/h, overtakes the motorist 42 s after the automobile passed him. Knowing that 18 s elapsed before the officer began pursuing the motorist, determine

(a) the distance the officer traveled before overtaking the motorist,
(b) the motorist's speed.

Answer 1

S = 0.5 km

velocity of motorist = 42.857 km/h

Step-by-step explanation:

given data

speed = 70 km/h

accelerates uniformly = 90 km/h

time = 8 s

overtakes motorist = 42 s

solution

we know initial velocity u1 of police = 0

final velocity u2 = 90 km/h = 25 mps

we apply here equation of motion

u2 = u1 + at

so acceleration a will be

a =
`(25-0)/(8)`

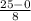
a = 3.125 m/s²

so

distance will be

S1 = 0.5 × a × t²

S1 = 100 m = 0.1 km

and

S2 = u2 × t

S2 = 25 × 16

S2 = 400 m = 0.4 km

so total distance travel by police

S = S1 + S2

S = 0.1 + 0.4

S = 0.5 km

and

when motorist travel with uniform velocity

than total time = 42 s

so velocity of motorist will be

velocity of motorist =
`(S)/(t)`

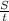
velocity of motorist =
`(500)/(42)`

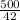
velocity of motorist = 42.857 km/h