Question

Followingisa statementof a theoremwhichcan beproven usingthequadratic formula. For this theorem, a, b, and c are real numbers. Theorem If f is a quadratic function of the form f .x/ D ax2 Cbx Cc and ac < 0, then the function f has two x-intercepts. Using only this theorem, what can be concluded about the functions given by the following formulas(a) g (x) = -8x^2 + 5x - 2 (b) h (x) = -(1/3)x^2 + 3x (c) k (x) = 8x^2 - 5x - 7 (d) j (x) = -(71/99)x^2 + 210 (e) f (x) = 4x^2 - 3x + 7 (f) F (x) = -x^4 + x^3 + 9

Answer 1

We have the following theorem:

If f is a quadratic function of the form
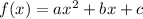`f(x)=ax^2+bx+c` and
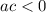`ac<0`, then the function f has two x-intercepts.

(a)
`g(x)=-8x^2+5x-2`

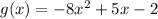
For this function a = -8 and c = -2, then
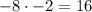`-8\cdot -2=16` is greater than zero. Therefore, we cannot conclude anything.

(b)
`h(x) =-(1)/(3)x^2+3x`

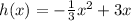
For this function a = -8 and we don't know the value of c. Therefore, we cannot conclude anything.

(c)
`k (x) = 8x^2 - 5x - 7`

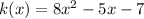
For this function a = 8 and c = -7, then
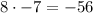`8\cdot -7=-56` is less than zero. Therefore, we can conclude that the function k has two x-intercepts.

(d)
`j(x)=-(71)/(99) x^2+210`

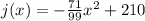
For this function a =
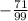`-(71)/(99)` and c = 210, then
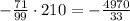`-(71)/(99)\cdot 210=-(4970)/(33)` is less than zero. Therefore, we can conclude that the function k has two x-intercepts.

(e)
`f(x)=4x^2-3x+7`

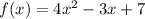
For this function a = 4 and c = 7, then
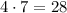`4\cdot 7=28` is greater than zero. Therefore, we cannot conclude anything.

(f)
`F(x)=-x^4+x^3+9`

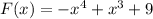
We cannot conclude anything because this is not a quadratic function.