Answer:
We have the following theorem:
If f is a quadratic function of the form
 and
and
 , then the function f has two x-intercepts.
, then the function f has two x-intercepts.
(a)
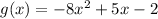
For this function a = -8 and c = -2, then
 is greater than zero. Therefore, we cannot conclude anything.
is greater than zero. Therefore, we cannot conclude anything.
(b)
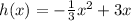
For this function a = -8 and we don't know the value of c. Therefore, we cannot conclude anything.
(c)
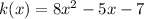
For this function a = 8 and c = -7, then
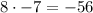 is less than zero. Therefore, we can conclude that the function k has two x-intercepts.
is less than zero. Therefore, we can conclude that the function k has two x-intercepts.
(d)
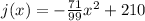
For this function a =
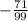 and c = 210, then
and c = 210, then
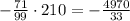 is less than zero. Therefore, we can conclude that the function k has two x-intercepts.
is less than zero. Therefore, we can conclude that the function k has two x-intercepts.
(e)
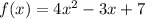
For this function a = 4 and c = 7, then
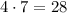 is greater than zero. Therefore, we cannot conclude anything.
is greater than zero. Therefore, we cannot conclude anything.
(f)
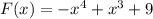
We cannot conclude anything because this is not a quadratic function.