Question

Suppose that you can throw a projectile at a large enough v0 so that it can hit a target a distance R downrange. Given that you know v0 and R, determine the general expressions for the two distinct launch angles θ1 and θ2 that will allow the projectile to hit D. For v0 = 37 m/s and R = 70 m, determine numerical values for θ1 and θ2.

Answer 1

`\theta_1=15^o\\\theta_2=75^o`

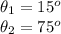
Step-by-step explanation:

Projectile Motion

In projectile motion, there are two separate components of the acceleration, velocity and displacement. The horizontal component has zero acceleration (assuming no friction), and the acceleration in the vertical direction is always the acceleration of gravity. The basic formulas are shown below:

`V_x=V_(ox)=V_ocos\theta`

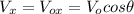
Where
`\theta` is the angle of launch respect to the positive horizontal direction and Vo is the initial speed.

`V_y=V_(oy)-gt=V_osin\theta-gt`

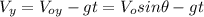
The horizontal and vertical distances are, respectively:

`x=V_(o)cos\theta t`

`\displaystyle y=y_o+V_(o)sin\theta t-(gt^2)/(2)`

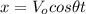
The total flight time can be found as that when y = 0, i.e. when the object comes back to ground (or launch) level. From the above equation we find

`\displaystyle t_f=(2V_osin\theta)/(g)`

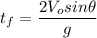
Using this time in the horizontal distance, we find the Range or maximum horizontal distance:

`\displaystyle R=(V_o^2sin2\theta)/(g)`

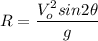
Let's solve for
`\theta`

`\displaystyle sin2\theta=(R.g)/(V_o^2)`

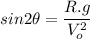
This is the general expression to determine the angles at which the projectile can be launched to hit the target. Recall the angle can have to values for fixed positive values of its sine:

`\displaystyle \theta_1=(asin\left((R.g)/(V_o^2)\right))/(2)`

`\displaystyle \theta_2=(180^o-asin\left((R.g)/(V_o^2)\right))/(2)`

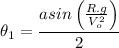
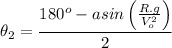
Or equivalently:

`\theta_2=90^o-\theta_1`

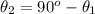
Given Vo=37 m/s and R=70 m

`\displaystyle \theta_1=(asin\left((70* 9.8)/(37^2)\right))/(2)`

`\theta_1=15^o`

And

`\theta_2=90^o-15^o=75^o`