Question

Rewrite each of the following sentences using logical connectives. Assume that each symbol!, x₀, n, x, B represents some fixed object.

(a) If f has a relative minimum at x₀ and if f is differentiable at x₀, then f′(x₀)=0..,
(b) If n is prime, then n = 2 or n is odd.,
(c) R is symmetric and transitive whenever R is irreflexive.,
(d) B is square and not invertible whenever det B = 0.,
(e) f has a critical point at x₀ iff f '(x₀) = 0 or f'(x₀) does not exist.,
(f) 2 < n - 6 is a necessary condition for 2n < 4 or n > 4.,
(g) 6 ≥ n - 3 only if n > 4 or n > 10.,
(h) x is Cauchy implies x is convergent.,
( i) f is continuous at x₀ whenever
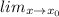
`lim_(x \rightarrow x_0)` f(x) = f(x₀).,
(j) If f is differentiable at x₀ and f is increasing at x₀, then f'(x₀) > 0.

Answer 1

a)
`(f\ has\ a\ relative \ minimum \ at\ x_(0) )` ∧
`(f\ is\ differenciable\ at\ x_(0) )` ⇒
`f^(') (x_(0) )=0`.

b)
`(n\ is\ prime)` ⇒
`(n=2)` ∨
`(n\ is \ odd)`.

c)
`R\ is \ irreflexive\` ⇒
`(R\ is\ symmetric)` ∧
`(R\ is\ transitive)`.

d)
`detB=0` ⇒
`(B \ is\ square)` ∧
`(B\ is\ not\ invertible)`.

e)
`f\ has\ a\ critical\ point\ at \ x_(0)` ⇔
`(f^(')(x_(0))=0)` ∨
`() \ f^(')(x_(0)) \ does\ not\ exist`.

f)
`2n<4` ∨
`n>4` ⇒
`2<n-6`.

g)
`6\geq n-3` ⇔
`n>4` ∨
`n>10`.

h)
`x \ is \ cauchy` ⇒
`x\ is\ convergent`.

i)
`\lim_{x \to \ x_(0)} f(x)=f(x_(0))` ⇒
`f\ is\ continous\ at \ x_(0)`.

j)
`(f\ is\ diferenciable\ at\ x_(0))` ∧
`(f\ is\ increasing\ at\ x_(0))` ⇒
`f^(')(x_(0))>0`.