Solve ( x + 1 < 5) ∩ ( x - 4 > -3).

Question

asked Jan 23, 2021 89.7k views

1 Answer

Robert Knight · Answer 1 · 2021-01-28T13:35:43+0000

The intersection of
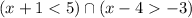$(x+1<5) \cap(x-4>-3)$ is
(1,4)

Step-by-step explanation:

The expression is
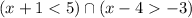
$(x+1<5) \cap(x-4>-3)$

To determine the intersection of these two inequalities, let us solve the two inequalities separately.

Consider
x+1<5

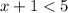
Subtracting both sides by 1, we have,

x<4

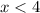
Also, consider
x-4>-3

Adding both sides by 4, we have,

x>1

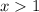
Using these two simplified inequalities in the expression, we have,

$(x<4) \cap(x>1)$

Writing this in the interval notation, we get,

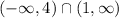
$(-\infty, 4) \cap(1, \infty)$

Hence, the intersection of the two interval is

(1,4)

Thus, the intersection of
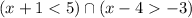$(x+1<5) \cap(x-4>-3)$ is
(1,4)