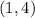Question

Solve ( x + 1 < 5) ∩ ( x - 4 > -3).

Answer 1

The intersection of
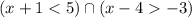`(x+1<5) \cap(x-4>-3)` is
`(1,4)`

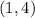
Step-by-step explanation:

The expression is
`(x+1<5) \cap(x-4>-3)`

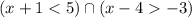
To determine the intersection of these two inequalities, let us solve the two inequalities separately.

Consider
`x+1<5`

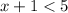
Subtracting both sides by 1, we have,

`x<4`

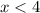
Also, consider
`x-4>-3`

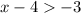
Adding both sides by 4, we have,

`x>1`

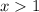
Using these two simplified inequalities in the expression, we have,

`(x<4) \cap(x>1)`

Writing this in the interval notation, we get,

`(-\infty, 4) \cap(1, \infty)`

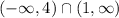
Hence, the intersection of the two interval is

`(1,4)`

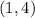
Thus, the intersection of
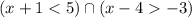`(x+1<5) \cap(x-4>-3)` is
`(1,4)`