Question

An object of mass 700700 kg is released from rest 20002000 m above the ground and allowed to fall under the influence of gravity. Assuming the force due to air resistance is proportional to the velocity of the object with proportionality constant bequals=5050 ​N-sec/m, determine the equation of motion of the object. When will the object strike the​ ground? [Hint: Here the exponential term is too large to ignore. Use​ Newton's method to approximate the time t when the object strikes the​ ground.] Assume that the acceleration due to gravity is 9.81 m divided by sec squared9.81 m/sec2.

Answer 1

59.503987 seconds

Step-by-step explanation:

b = Proportionality constant = 50 Ns/m

g = Acceleration due to gravity = 9.81 m/s²

m = Mass of object = 700 kg

We have the equation of velocity

`v(t)=(mg)/(b)+\left(V_0-(mg)/(b)\right)e^{(bt)/(m)}`

The equation of motion

`x(t)=(mg)/(b)+(m)/(b)\left(V_0-(mg)/(b)\right)(1-e^{(bt)/(m)})`

`x(t)=(700* 9.81)/(50)+(9.81)/(50)\left(0-(700* 9.81)/(50)\right)(1-e^{(50t)/(700)})`

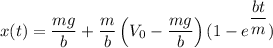
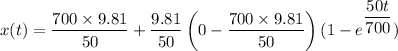
when x(t)=2000

`2000=(700* 9.81)/(50)+(9.81)/(50)\left(0-(700* 9.81)/(50)\right)(1-e^{(50t)/(700)})\\\Rightarrow 2000* \:50=(700* \:9.81)/(50)* \:50+(9.81)/(50)\left(0-(700* \:9.81)/(50)\right)\left(1-e^{(50t)/(700)}\right)* \:50\\\Rightarrow 6867-(67365.27)/(50)\left(1-e^{(50t)/(700)}\right)=100000\\\Rightarrow 50\left(-(67365.27)/(50)\left(1-e^{(50t)/(700)}\right)\right)=93133* \:50\\\Rightarrow \frac{-67365.27\left(1-e^{(50t)/(700)}\right)}{-67365.27}=(4656650)/(-67365.27)\\\Rightarrow 1-e^{(50t)/(700)}=-69.12538\dots\\\Rightarrow -e^{(50t)/(700)}=-70.12538\dots\\\Rightarrow t=14\ln \left(70.12538\dots \right)\\\Rightarrow t=59.50398\ s`

The time taken is 59.503987 seconds