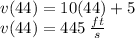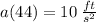Question

Given s left parenthesis t right parenthesis equals 5 t squared plus 5 ts(t)=5t2+5t​, find

​(a)
​v(t). ​ (b) ​ a(t).
​(c)
the velocity and acceleration when tequals=44.
​(a) ​v(t)equals=nothing
​(b) ​a(t)equals=nothing
​(c) When tequals=44​, the velocity is nothing feet per second.
​(Simplify your​ answer.)
When tequals=44​, the acceleration is nothing feet per second squared.

Answer 1

The velocity function is
`v(t)=10t+5`.

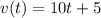The acceleration function is
`a(t)=10`.

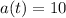When t = 44​, the velocity is
`v(44)=445 \:(ft)/(s)`.

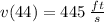When t = 44​, the acceleration is
`a(44)=10\: (ft)/(s^2)`.

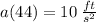Explanation:

We know that the position function is given by

`s(t)=5t^2+5t`

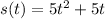
Velocity is defined as the rate of change of position or the rate of displacement. If you take the derivative of the position function you get the instantaneous velocity function.

`v(t)=(ds)/(dt)`

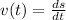
Acceleration is defined as the rate of change of velocity. If you take the derivative of the instantaneous velocity function you get the instantaneous acceleration function.

`a(t)=(dv)/(dt)`

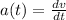
The instantaneous velocity function is given by

`v(t)=(d)/(dt) s(t)=(d)/(dt)(5t^2+5t)\\\\\mathrm{Apply\:the\:Sum/Difference\:Rule}:\quad \left(f\pm g\right)'=f\:'\pm g'\\\\v(t)=(d)/(dt)\left(5t^2\right)+(d)/(dt)\left(5t\right)\\\\\mathrm{Apply\:the\:Power\:Rule}:\quad (d)/(dx)\left(x^a\right)=a\cdot x^(a-1)\\\\v(t)=10t+(d)/(dt)\left(5t\right)\\\\\mathrm{Apply\:the\:common\:derivative}:\quad (d)/(dt)\left(t\right)=1\\\\v(t)=10t+5`

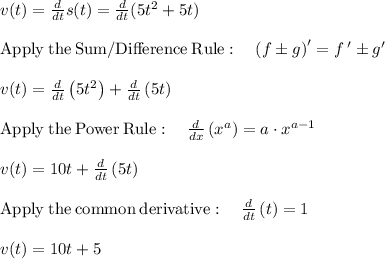
The instantaneous acceleration function is given by

`a(t)=(dv)/(dt) =(d)/(dt)(10t+5)\\\\\mathrm{Apply\:the\:Sum/Difference\:Rule}:\quad \left(f\pm g\right)'=f\:'\pm g'\\\\a(t)=(d)/(dt)\left(10t\right)+(d)/(dt)\left(5\right)\\\\a(t)=10`

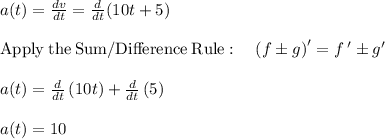
To find the velocity and acceleration when t = 44, we substitute this value into the velocity and acceleration functions

`v(44)=10(44)+5\\v(44)=445 \:(ft)/(s)`

`a(44)=10\: (ft)/(s^2)`