Answer:
(a) Approximately 205 students scored between 540 and 660.
(b) Approximately 287 students scored between 480 and 720.
Explanation:
A mound-shaped distribution is a normal distribution since the shape of a normal curve is mound-shaped.
Let X = test score of a student.
It is provided that
 .
.
(a)
The probability of scores between 540 and 660 as follows:
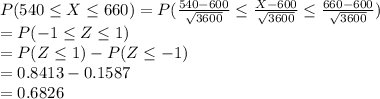
Use the standard normal table for the probabilities.
The number of students who scored between 540 and 660 is:
300 × 0.6826 = 204.78 ≈ 205
Thus, approximately 205 students scored between 540 and 660.
(b)
The probability of scores between 480 and 720 as follows:
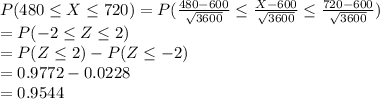
Use the standard normal table for the probabilities.
The number of students who scored between 480 and 720 is:
300 × 0.9544 = 286.32 ≈ 287
Thus, approximately 287 students scored between 480 and 720.