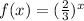Question

Create an equation that matches the table

Answer 1

The equation that matches the table is
`f(x)=((2)/(3) )^(x)`

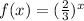
Step-by-step explanation:

From the table, we can see that this is a geometric progression because the common difference in the y-term is
`(2)/(3)`

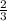
Thus,
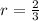`r=(2)/(3)` and
`a=(2)/(3)`

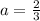
To determine the equation, let us substitute the values of r and a in the general form of geometric progression.

The general form of geometric progression is given by

`a_(n)=a r^(n-1)`

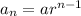
Now, substituting we have,

`a_(n)=(2)/(3)\left((2)/(3)\right)^(n-1)`

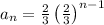
Simplifying by adding the powers of similar terms, we get,

`a_(n)=((2)/(3))^(n)`

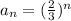
Writing it in terms of x, we get,

`f(x)=((2)/(3) )^(x)`

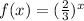
Thus, the equation that matches the given table is
`f(x)=((2)/(3) )^(x)`