Question

A cube is 3 cm on a side, with one corner at the origin. What is the unit vector pointing from the origin to the diagonally opposite corner at location <3,3,3> cm? what is the angle from this disagonal to one of the adjacent edges of the cubes?

Answer 1

0.955 rad or 54.7 degrees

Step-by-step explanation:

The vector (let's call it's A) pointing from the origin to the diagonally opposite corner would have its value of:

`\vec{A} = <3,3,3>`

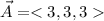
but unit vector only has a length of 1, so we need to divide this vector by length of itself to it has the same direction but magnitude of 1

`|A| = √(3^2 + 3^2 +3^2) = √(27) = 3√(3)`

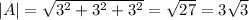
So the unit vector in the direction of vector A is

`\vec{a} = \frac{\vec{A}}A = <(1)/(√(3)),(1)/(√(3)),(1)/(√(3))>`

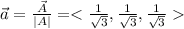
Let another unit vector b <0,0,1> lies in the adjacent edges of the cubes. This unit vector also has a length of 1. So |b| = 1.The dot product between a and b yields

`a \cdot b = |a||b|cos\theta`

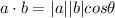
where Θ is the angle between vector a and b

`a \cdot b = <(1)/(√(3)),(1)/(√(3)),(1)/(√(3))> <0,0,1> = 0 + 0 + (1)/(√(3)) = (1)/(√(3))`

`|a||b|cos\theta = 1*1*cos\theta`

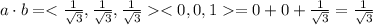
therefore
`cos\theta = (1)/(√(3))`

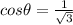
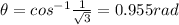`\theta = cos^(-1)(1)/(√(3)) = 0.955 rad` or 54.7 degrees