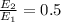Answer:
0.5
Step-by-step explanation:
The energy of a charged capacitor is given by
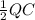 where
where
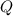 is the charge on it and
is the charge on it and
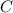 is its capacitance. The capacitance is defined, geometrically, as
is its capacitance. The capacitance is defined, geometrically, as
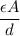
where
 is a constant that is determined by the material between the plates,
is a constant that is determined by the material between the plates,
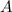 is the area of the plates and
is the area of the plates and
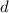 is the distance between them. It is then that the capacitance is linearly inversely proportional to the separation distance; as the distance increases, the capacitance reduces.
is the distance between them. It is then that the capacitance is linearly inversely proportional to the separation distance; as the distance increases, the capacitance reduces.
Because it is linear, when the separation distance is doubled, other factors remaining constant, the capacitance is halved. Because the capacitance is halved, the energy is halved.
Let's see the mathematics.
Initial capacitance,
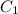 at initial separation,
at initial separation,
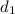
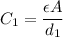
If separation is doubled, separation becomes
 . Then the capacitance becomes
. Then the capacitance becomes
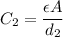
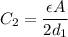
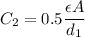
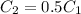
Initial energy,
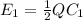
Final energy,
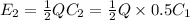
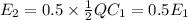
Hence,