Question

If two cards are drawn at random without replacement, show that the correlation coefficient betwen the numbers appearing on the two cards is -1(N-1).

Answer 1

The proof is in the explanation below.

Explanation:

Data:

Let N cards have different numbers: x₁, x₂,x₃.....xn

To calculate the correlation coefficient p, let the two random variable be defined as C₁ and C₂.

These variables represent the different number x₁ on the card 1 and card 2 respectively.

Let also the indicative factors be
`I_(C1=X1)` and
`I_(C2 = x1)`

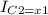
Therefore:

E[1C1=xi]=Pr[C1=xi]=1N

E[1C2=xi]=Pr[C2=xi]=Pr[C2=xi∣C1≠xi]Pr[C1≠xi]=1NandE[1C1=xi1C2=xj]=Pr[C1=xi∩C2=xj]= -1(N−1)