Question

If an object is near the surface of the earth the variation of its weight with distance from the center of the earth can ofteb be neglected the acceleration due to gravity at sea level is g = 9.81 m/s^2 the radius of the earth is 6370 km the weight of an object at sea level is mg where m is its mass.

a. At what height above the surface of the earth deos the weight of the object decrease to 0.99mg?

Answer 1

h=32.1 km

Step-by-step explanation:

solution:

using newton law of gravitational attraction and newton second law:

`W=(Gmm_(E) )/(r^(2) ) \\a=(Gm_(E))/(r^(2)) \\W=ma\\`

`m_(E)= mass of earth`

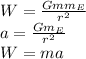
r= distance between two masses

at sea level

a=g

`r=R_(E)`

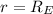
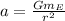`a=(Gm_(E))/(r^(2))`.............................(1)

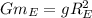`Gm_(E) =gR_(E)^2`.........................(2)

by substituting (2) and (1)
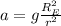`a=g(R_(E)^2 )/(r^(2) )` acceleration due to gravity at a distance r from the centre of the earth in terms of g (sea level)

so the weight of the object at a distance r from the centre of the earth (W=ma)

W=mg(Re^2/r^2)..........(3)

h the height above the surface of the earth: r=Re+h

putting the value of r in eq (3)

W=mg(Re/Re+h)^2

W=0.99 mg

solving for height h:

h=Re(1/√0.99)-(1))

h=32.1 km