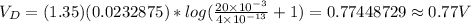Question

A semiconductor diode has the following parameters: Is = 4.0×10-13 Amps, n = 1.35, and is operated at a temperature of T = 270K. (a) Find the value of the thermal voltage VT. (b) What is the diode current I when the diode voltage is V = 0.6V? (c) What is the diode voltage when the current is I = 20 mA?

Answer 1

`V_T=0.02328V\\I=7.77* 10^(-5) A \\V_D=0.77V`

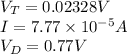
Step-by-step explanation:

Let's use Shockley ideal diode equation which relates the current intensity and the potential difference:

`I=I_S (e^{(V_D)/(nV_T) } -1)`

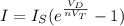
Where:

`I=Diode\hspace{3}current\\I_S=Reverse\hspace{3}bias\hspace{3}saturation\hspace{3}current\\V_D=Voltage\hspace{3}across\hspace{3}the\hspace{3}diode\\V_T=Thermal\hspace{3}voltage\\n=Ideality\hspace{3}factor`

Thermal voltage at any temperature it is a known constant defined by:

`V_T=(kT)/(q)`

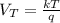
Where:

`k= Boltzmann\hspace{3}constant \approx1.38* 10^(-23) \\T=Absolute\hspace{3}temperature\\q=Charge\hspace{3}of\hspace{3}an\hspace{3}electron \approx 1.6* 10^(-19) C`

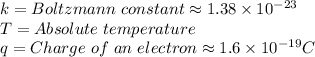
(a)

Using the data provided:

`V_T=((1.38* 10^(-23))*(270) )/(1.6* 10^(-19) )= 0.0232875V`

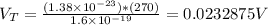
(b)

Using the data provided and Shockley ideal diode equation

`I=(4* 10^(-13) )*(e^{(0.6)/(1.35*0.0232875) }-1)=7.773505834*10^(-5)\approx 7.77 *10^(-5)A\\I\approx0.0777mA`

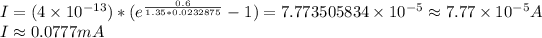
(c) Let's isolate
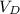`V_D` from Shockley ideal diode equation:

`I=I_S (e^{(V_D)/(nV_T) } -1)\\\\Multiply\hspace{3}both\hspace{3}sides\hspace{3}by\hspace{3}I_S\\\\\ (I)/(I_S) = e^{(V_D)/(nV_T) } -1\\\\Add\hspace{3}1\hspace{3}both\hspace{3}sides\\\\`

`(I)/(I_S) +1 =e^{(V_D)/(nV_T) } \\\\Take\hspace{3}the\hspace{3}natural\hspace{3}logarithm\hspace{3}of\hspace{3}both\hspace{3}sides\\\\(V_D)/(nV_T) =log((I)/(I_S) +1) \\\\Multiply\hspace{3}both\hspace{3}sides\hspace{3}by\hspace{3}nV_T\\\\V_D=nV_T*log((I)/(I_S) +1)`

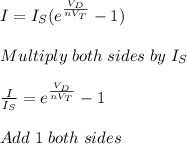
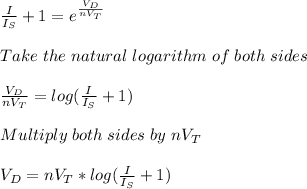
Finally, using the data provided:

`V_D=(1.35)(0.0232875)*log((20* 10^(-3) )/(4* 10^(-13) )+1)=0.77448729\approx 0.77V`